https://school.programmers.co.kr/learn/courses/30/lessons/67259
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
이 문제는 처음에 2차원 DP + DFS로 접근했지만 2차원으로는 해결할 수 없는 문제가 있었다. 그래서 해당 접근은 보류하고 처음부터 다시 생각했고, 방향에 따라서 간선의 가중치가 달라진다는 점과 최단 거리를 구해야한다는 점을 토대로 다익스트라 알고리즘을 사용해서 문제를 풀었다.
이 문제는 진행 방향에 따라서 도로 건설 비용이 달라질 수 있음을 고려해주어야 한다. 아래는 문제에서 설명을 위해 첨부한 그림이다.
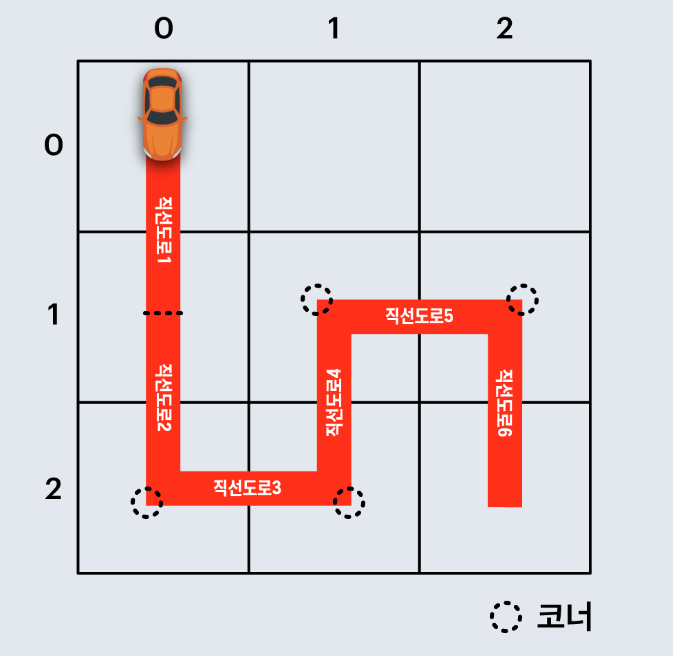
위 그림을 살펴보면 자동차가 직진하는 경우에는 직선도로 한 개가 필요하지만 다른 방향으로 꺾어서 진행하는 경우에는 코너와 직선도로가 모두 필요하다. 즉 직진인 경우에는 100원, 꺾는 경우에는 600원이 든다고 볼 수 있다. 이를 토대로 방향을 고려하여 금액을 누적시키면서 최단 거리를 구하면 된다.
탐색을 시작할 땐 방향을 -1로 설정하고 코드 내에서 진입 방향이 -1인 경우 비용을 100원으로 설정해주었다. (출발 지점에서는 모든 곳으로 직진할 수 있기 때문이다)
#include <string>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INF (int)1e9
int dy[] = {-1, 0, 1, 0};
int dx[] = {0, 1, 0, -1};
int N;
int dist[26][26]; // 현재 위치까지의 최단 비용
struct Pos {
int cost;
int y;
int x;
int dir;
Pos(int c, int y_, int x_, int d):cost(c), y(y_), x(x_), dir(d) {}
bool operator<(const Pos& p) const {
return cost < p.cost;
}
};
inline bool oor(int& y, int& x) {
return (y < 0 || x < 0 || y >= N || x >= N);
}
int dijkstra(vector<vector<int>>& board) {
priority_queue<Pos> pq;
dist[0][0] = 0;
pq.emplace(0, 0, 0, -1);
while(!pq.empty()) {
auto y = pq.top().y;
auto x = pq.top().x;
auto dir = pq.top().dir;
auto cost = pq.top().cost;
pq.pop();
if(dist[y][x] < cost) continue;
for(int i = 0; i < 4; i++) {
int ny = y + dy[i];
int nx = x + dx[i];
if(oor(ny, nx) || board[ny][nx]) continue;
int nc = cost + (dir == i ? 100 : 600);
if(dir == -1) nc = 100;
if(dist[ny][nx] >= nc) {
dist[ny][nx] = nc;
pq.emplace(nc, ny, nx, i);
}
}
}
return dist[N - 1][N - 1];
}
int solution(vector<vector<int>> board) {
N = board.size();
fill_n(dist[0], 26 * 26, INF);
return dijkstra(board);
}'알고리즘 & 자료구조 > 문제 풀이' 카테고리의 다른 글
| 백준 1033.cpp [칵테일] (0) | 2022.05.17 |
|---|---|
| 백준 7579.cpp [앱] (0) | 2022.04.22 |
| 백준 2110.cpp (매개변수 탐색) (0) | 2022.03.29 |
| 백준 2098.cpp [외판원 순회] (0) | 2022.03.26 |
| 17142.cpp (0) | 2022.02.08 |
