크루스칼 알고리즘은 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘이다. 최소 비용 신장 트리를 만들기 위한 대표 알고리즘이라고 할 수 있다. 흔히 여러 개의 도시를 최소한의 비용으로 도로를 설치하고자 할 때 실제로 사용되는 알고리즘이라고 한다.
최소 비용 신장 트리란? [Minimum Spanning Tree]
우선 신장 트리란(Spanning Tree) 그래프의 최소 연결 부분 그래프이다. 특징으로는 모든 정점을 포함해야 한다는 것과 가장 적은 간선 개수로 모든 정점을 연결해야 한다는 특징이 있다.
최소 비용 신장 트리란 신장 트리의 특징을 포함하며, 간선의 가중치를 고려해서 최소한의 비용으로 신장 트리를 구성해야한다는 특징을 가지고 있다. 따라서 구성된 그래프의 간선의 합이 최소여야 하고 사이클이 포함되어서는 안 된다. (최소한의 간선과 가중치로 그래프를 구성해야 하는데 사이클이 생길 이유가 없다)
최소 비용 신장 트리는 줄여서 MST라고 부른다.
크루스칼 알고리즘의 동작 과정을 그림으로 살펴보자.
다음과 같은 그래프가 있다고 할 때, 먼저 그래프의 간선들을 비용 순으로 오름차순 정렬해야 한다.
(그래프에 간선의 방향은 신경 쓸 필요가 없다)
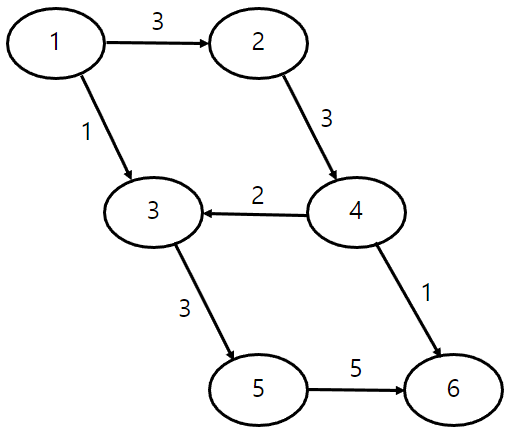
간선들을 오름차순 정렬하면 다음과 같다.

이제 정렬된 간선들을 차례대로 그래프에 포함시키면 되는데 이때 주의할 점이 있다. Minimum Spaninng Tree에서 설명했듯이 그래프에는 사이클이 형성되면 안 된다. 따라서 사이클을 감지할 수 있어야 하는데 Union Find 알고리즘을 사용하면 쉽게 구현할 수 있다.
https://braindisk.tistory.com/13
Union find
Union find - 합집합을 찾는 대표적인 그래프 알고리즘이다. 합집합 여부를 판별할 수 있기 때문에 서로소 집합 여부도 판별할 수 있어 서로소 집합(Disjoint-set) 알고리즘이라고도 한다. Union find는 여
braindisk.tistory.com
일단 사이클이 형성될 위험이 없으므로 우선 두개의 간선을 포함시키자.
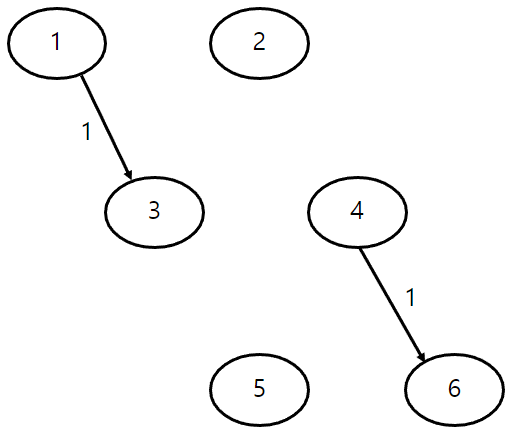


다음으로 4-3 비용 2의 간선을 포함시키자. 사이클이 형성되지 않으므로 문제가 없다.
1-2 비용 3의 간선 또한 포함시켜도 사이클이 형성되지 않을 것이다. 함께 포함시킨다.



벌써 한 개의 노드를 제외하고 모든 노드가 연결되었다.. 너무 그래프를 쉽게 그렸나
이제 다음으로 2-4 비용 3의 간선을 살펴보자. 이 간선을 포함할 경우 사이클이 형성될 수 있으므로 포함하지 않고 건너뛴다.


다음으로 3-5 비용 3의 간선은 포함시켜도 문제되지 않는다.


다음으로 5-6 비용 5의 간선은 딱 봐도 사이클이 형성된다 ㅎㅎ
이것으로 모든 노드가 최소한의 간선과 비용으로 연결되었다. 크루스칼의 알고리즘을 코드로 구현해보자.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int findParent(int* parent, int now) {
if(parent[now] == now) return now;
return parent[now] = findParent(parent, parent[now]);
}
void unionParent(int* parent, int a, int b) {
a = findParent(parent, a);
b = findParent(parent, b);
if(a > b) parent[parent[a]] = b;
else parent[parent[b]] = a;
}
bool checkParent(int* parent, int a, int b) {
return findParent(parent, a) == findParent(parent, b);
}
struct Edge {
int start;
int end;
int cost;
Edge(int s, int e, int c) : start(s), end(e), cost(c) {}
};
int main() {
// 노드 개수
const int nodes = 6;
// 간선 정보를 입력받는다
vector<Edge> edges;
edges.emplace_back(5, 6, 5);
edges.emplace_back(3, 5, 3);
edges.emplace_back(2, 4, 3);
edges.emplace_back(1, 2, 3);
edges.emplace_back(4, 3, 2);
edges.emplace_back(4, 6, 1);
edges.emplace_back(1, 3, 1);
sort(edges.begin(), edges.end(), [](Edge a, Edge b) {
if(a.cost < b.cost) return true;
else if(a.cost == b.cost) {
return a.start > b.start;
}
return false;
});
int parent[nodes];
for(int i = 0; i < nodes; i++) parent[i] = i;
int sum = 0;
for(int i = 0; i < edges.size(); i++) {
if(!checkParent(parent, edges[i].start - 1, edges[i].end - 1)) {
cout << "select >> " << edges[i].start << ", " << edges[i].end << ", " << edges[i].cost << endl;
sum += edges[i].cost;
unionParent(parent, edges[i].start - 1, edges[i].end - 1);
}
}
cout << "sum : " << sum << endl;
}
// 출력 결과
select >> 4, 6, 1
select >> 1, 3, 1
select >> 4, 3, 2
select >> 3, 5, 3
select >> 2, 4, 3
sum : 10선택된 간선과 비용의 합을 확인하면 잘 구현된 것을 볼 수 있다. Union Find 알고리즘을 안다면 어렵지 않게 구현이 가능한 알고리즘 같다.
크루스칼 알고리즘의 시간 복잡도는 정렬 알고리즘의 시간 복잡도와 같다. 어떤 정렬 알고리즘을 사용하느냐에 따라서 달라진다.
reference
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 힙 정렬 (0) | 2022.03.16 |
|---|---|
| 위상 정렬 (0) | 2022.03.11 |
| 플루이드 와샬 (0) | 2022.03.02 |
| Union find (0) | 2022.02.28 |
| Trie 자료구조 (0) | 2022.02.28 |
