Union find - 합집합을 찾는 대표적인 그래프 알고리즘이다. 합집합 여부를 판별할 수 있기 때문에 서로소 집합 여부도 판별할 수 있어 서로소 집합(Disjoint-set) 알고리즘이라고도 한다.
Union find는 여러 개의 노드가 있을 때 두 노드를 선택해서, 현재 같은 그래프(집합)에 속하는지를 판별하는 알고리즘이다. 현재 같은 그래프에 속하는지 여부는 부모를 통해서 알 수 있는데 부모가 같다면 같은 그래프(집합)에 속한다고 볼 수 있는 것이다. 그럼 각 노드 별로 부모를 어떻게 설정하고 비교할 수 있는지 확인해보자.
먼저 아래와 같이 노드가 있다고 하자.
처음에는 모든 노드가 자기 자신을 부모로 설정한다.

그리고 다음과 같이 1과 2가 Union(합침)되면 2의 부모가 1로 변하게 된다.
즉, 서로 다른 노드가 Union 되면서 그래프가 형성되었을 때, 해당 그래프에서 가장 작은 숫자의 노드가 전체 노드의 부모가 된다.
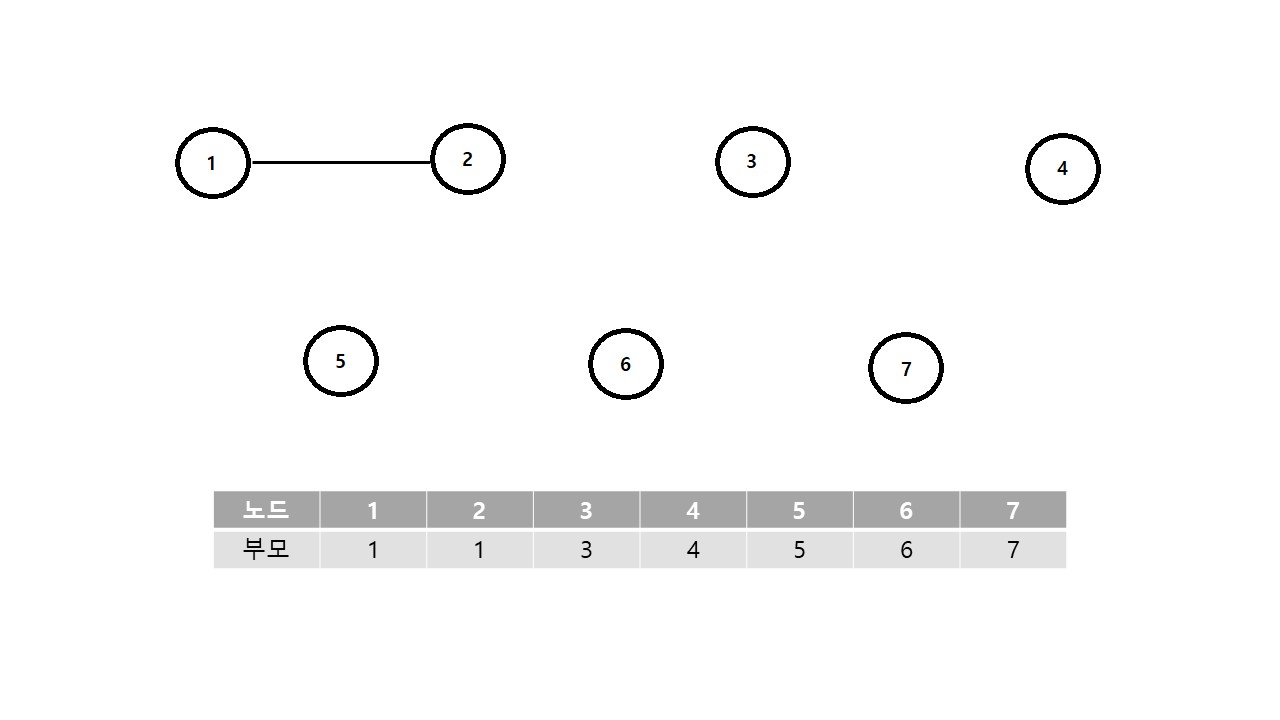
따라서 다음과 같이 진행된다.
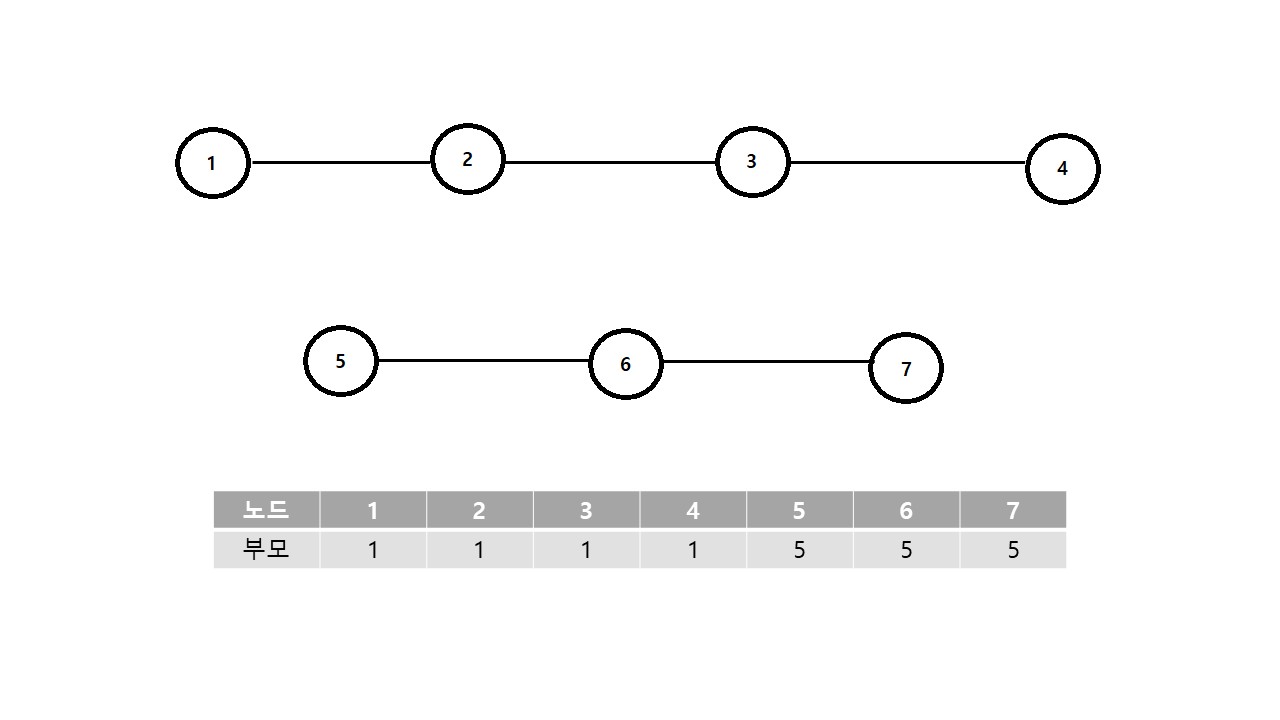
이때, 두 그래프를 잇게 되면 다음과 같이 부모가 변하게 된다.
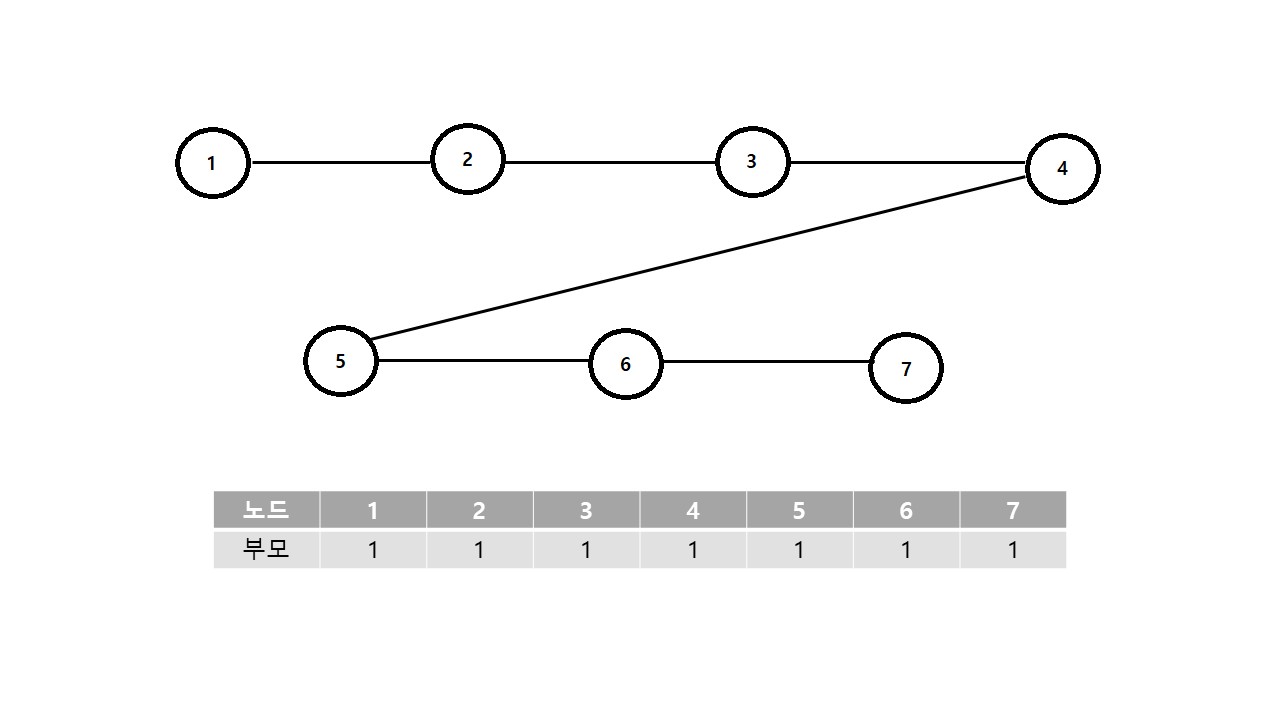
특징은 어떻게 연결되더라도 가장 작은 노드의 번호가 그래프에 속한 전체 노드의 부모로 지정된다는 것이다.
Union-find는 이렇게 부모를 설정할 때 서로 연결된 노드들을 재귀적으로 탐색하여 부모를 갱신한다.
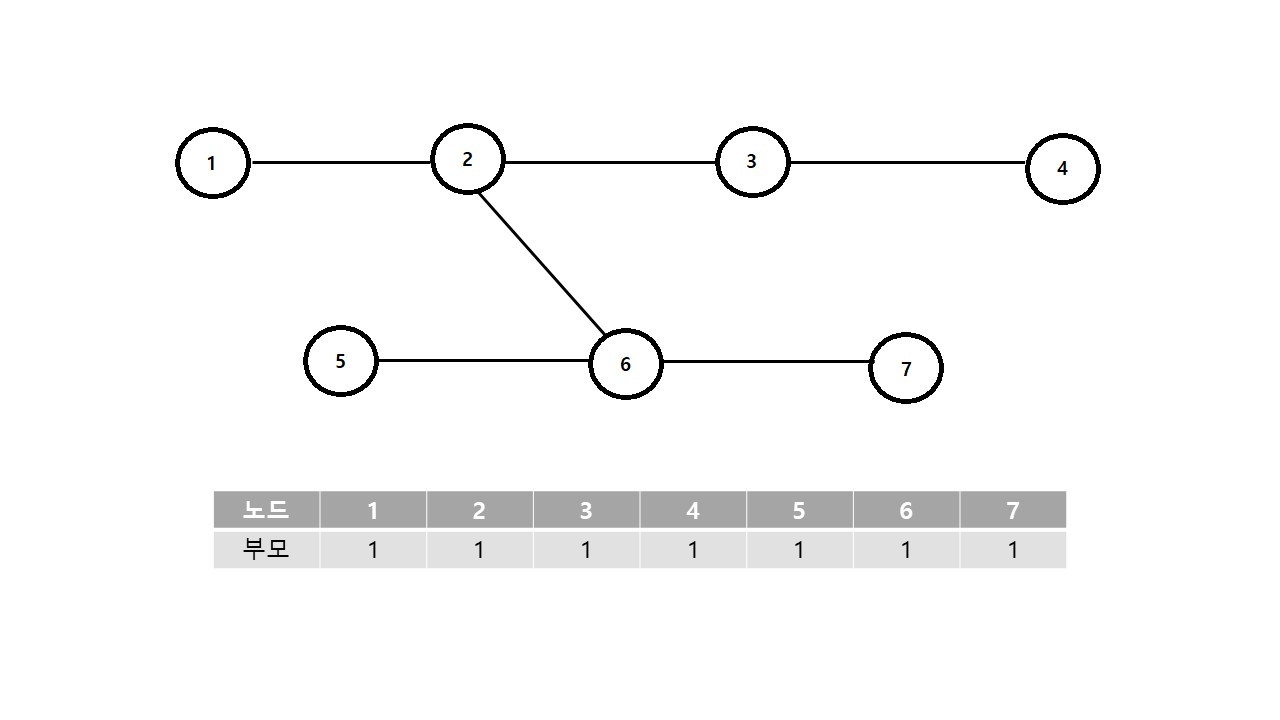
결론적으로 Union-find는 그래프의 연결 형태를 신경 쓸 필요 없이 합집합 여부와 서로소 집합 여부를 쉽게 판별할 수 있다.
그럼 Union-find에서 노드를 연결하는 것과 부모를 찾고, 갱신하는 작업이 어떻게 이루어지는지 구현해보자.
먼저 특정 노드의 부모를 찾는 메서드이다. 메서드를 살펴보면 주어진 노드의 부모와 부모의 부모 노드가 다를 경우 재귀적으로 탐색해서 부모 노드를 갱신하고 있다.
int findParent(int* parent, int now) {
if(parent[now] == now) return now;
return parent[now] = findParent(parent, parent[now]); // 재귀 탐색
}다음으로 서로 다른 두 노드를 합치는 메서드이다. 먼저 두 노드의 부모 노드를 구하고 더 작은 부모 노드의 번호를 부모 노드로 설정한다. 그리고 뒤에 자식들의 부모 값이 갱신되지 않더라도 추후에 findParent 메서드를 호출하면 재귀적으로 갱신되기 때문에 아무 문제가 없다.
void unionParent(int* parent, int a, int b) {
a = findParent(parent, a);
b = findParent(parent, b);
if(a < b) parent[b] = a;
else parent[a] = b;
}다음으로 같은 부모를 가지는지 확인하는 메서드이다.
이 메서드를 통해서 우리는 합집합 여부(서로소 집합 여부)를 확인할 수 있는 것이다.
bool checkParent(int* parent, int a, int b) {
int a = findParent(parent, a);
int b = findParent(parent, b);
return a == b;
}
위에서 구현한 메서드들을 종합해서 테스트를 해보자.
#include <iostream>
using namespace std;
int findParent(int* parent, int now) {
if(parent[now] == now) return now;
return now = findParent(parent, parent[now]);
}
void unionParent(int* parent, int a, int b) {
a = findParent(parent, a);
b = findParent(parent, b);
if(a < b) parent[b] = a;
else parent[a] = b;
}
bool checkParent(int* parent, int a, int b) {
a = findParent(parent, a);
b = findParent(parent, b);
return a == b;
}
void printParent(int* parent) {
cout << "node\t";
for(int i = 1; i < 11; i++) cout << i << ' ';
cout << endl << "parent\t";
for(int i = 1; i < 11; i++) cout << parent[i] << ' ';
cout << "\n_________________________________________________\n";
}
int main() {
int parent[11];
for(int i = 1; i < 11; i++) parent[i] = i;
// 처음 부모 노드 출력
printParent(parent);
/*
출력 결과
node 1 2 3 4 5 6 7 8 9 10
parent 1 2 3 4 5 6 7 8 9 10
*/
// 1과 2를 연결
unionParent(parent, 1, 2);
printParent(parent);
/*
출력 결과
node 1 2 3 4 5 6 7 8 9 10
parent 1 1 3 4 5 6 7 8 9 10
*/
// 3과 4, 4와 5, 5와 6을 연결
unionParent(parent, 3, 4);
unionParent(parent, 4, 5);
unionParent(parent, 5, 6);
printParent(parent);
/*
출력 결과
node 1 2 3 4 5 6 7 8 9 10
parent 1 1 3 3 3 3 7 8 9 10
*/
// 2와 6을 연결
unionParent(parent, 2, 6);
printParent(parent);
/*
출력 결과
node 1 2 3 4 5 6 7 8 9 10
parent 1 1 1 3 3 3 7 8 9 10
*/
}마지막 결과를 보면 아직 부모 노드 번호가 갱신되지 않은 노드들도 있다. 당연한 것이고 findParent 메서드를 호출하면 저절로 갱신될 것이다.
Union-find는 Strongly Connected Component와 같은 고급 알고리즘의 기초가 된다고 한다. 기초 알고리즘이라 그런지 쉽다는 느낌이 들고 여러 가지 문제에 유용하게 쓰일 수 있을 것 같다.
reference
https://www.youtube.com/watch?v=AMByrd53PHM
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 위상 정렬 (0) | 2022.03.11 |
|---|---|
| Kruskal Algorithm (0) | 2022.03.02 |
| 플루이드 와샬 (0) | 2022.03.02 |
| Trie 자료구조 (0) | 2022.02.28 |
| 밸만-포드 알고리즘 (0) | 2022.02.24 |
