위상 정렬(Topology Sort)는 순서가 정해져 있는 작업들의 수행 순서를 정해주기 위한 알고리즘이다.
예를 들어서 숫자가 하나의 작업이라고 했을 때, 다음과 같이 작업의 순서가 정해져 있다고 가정하자.
1 -> 3 -> 4
3 -> 2
그럼 (1 -> 3 -> 4 -> 2) 또는 (1 -> 3 -> 2 -> 4) 순서로 작업을 수행해야 함을 알 수 있다. 이렇게 정해진 순서를 고려해서 작업의 수행 순서를 결정해주는 알고리즘을 위상 정렬이라고 한다.
주의할 점은 위상 정렬은 DAG(Directed Acyclic Graph) 에만 적용이 가능하다. 위상 정렬이 "작업의 순서를 고려한다"는 점을 생각해보면 당연한 것이다. 사이클이 존재하는 것은 출발 지점이 따로 없다는 것이고 순서도 없다는 의미가 된다. 즉, 단방향 간선만을 가지고 사이클이 형성되지 않는 그래프에만 위상 정렬을 적용할 수 있다.

위상 정렬은 다음과 같은 순서로 동작한다.
- 진입 차수가 0인 노드를 큐에 삽입한다.
- 큐에서 노드를 꺼내 모든 간선을 삭제한다.
- 간선 제거로 인해 진입 차수가 0이 된 노드를 큐에 삽입한다.
- 모든 원소에 대해서 2~3 과정을 반복한다. 만약 모든 원소를 순회하기 전에 큐가 빈다면 그래프 내에 사이클이 존재한다는 것이다. 모든 원소를 방문했다면 큐에서 노드를 꺼낸 순서가 위상 정렬의 결과이다.
그럼 위상 정렬의 동작 과정을 그림으로 살펴보자. 먼저 고려해야 할 작업들의 순서는 다음과 같다.
1 -> 3 -> 4 -> 6
3 -> 7 -> 6
그래프로 나타내면 다음과 같다.
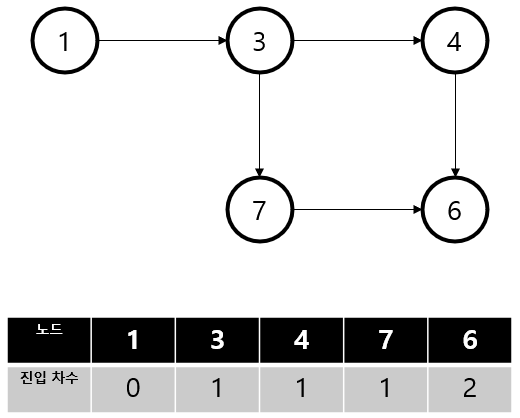
이제 진입 차수가 0인 1번 노드를 큐에 넣고 간선을 제거한다.

1번 노드의 간선이 제거되면서 3번 노드의 진입 차수가 0이 됐다. 3번 노드를 큐에 넣고 간선을 제거한다.

이제 4번, 7번 노드의 진입 차수가 0이 되었다. 4번, 7번 노드를 큐에 삽입하고 4번 노드를 꺼내서 간선을 제거한다.

다음으로 7번 노드를 꺼내서 간선을 제거한다.

따라서 결과는 다음과 같이 1 -> 3 -> 4 -> 7 -> 6 이 된다. (큐 삽입 순서에 따라 1 -> 3 -> 7 -> 4 -> 6 도 가능)
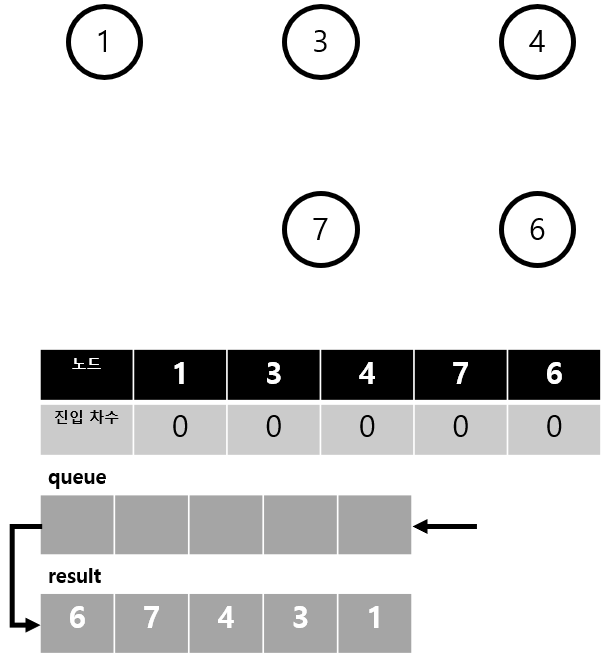
그럼 위상 정렬을 코드로 구현해보자.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define MAX 10
int n = 5;
int inDegree[MAX];
vector<int> edges[MAX];
void topologySort() {
queue<int> vq;
for(int i = 0; i < MAX; i++)
if(inDegree[i] == 0)
vq.emplace(i);
for(int i = 0; i < n; i++) {
if(vq.empty()) {
cout << "그래프 내에 사이클이 존재합니다.\n";
return;
}
// 큐에서 노드를 꺼낸다
int now = vq.front();
vq.pop();
// print result
cout << now << ' ';
// 해당 노드의 간선을 제거
for(int j = 0; j < edges[now].size(); j++) {
if(--inDegree[edges[now][j]] == 0) {
// 진입 차수가 0이 되었다면 큐에 삽입
vq.emplace(edges[now][j]);
}
}
}
}
inline int reset(int num) {
return (num == -1 ? 0 : num);
}
int main() {
// initial set
fill_n(inDegree, MAX, -1);
inDegree[1] = 0;
edges[1].emplace_back(3);
inDegree[3] = reset(inDegree[3]) + 1;
edges[3].emplace_back(4);
inDegree[4] = reset(inDegree[4]) + 1;
edges[3].emplace_back(7);
inDegree[7] = reset(inDegree[7]) + 1;
edges[4].emplace_back(6);
inDegree[6] = reset(inDegree[6]) + 1;
edges[7].emplace_back(6);
inDegree[6] = reset(inDegree[6]) + 1;
topologySort();
}
//출력 결과
1 3 4 7 6
위상 정렬의 시간 복잡도는 O(V + E)라고 한다. 즉 정점의 개수 + 간선의 개수만큼 소요된다.
빠르다!
reference
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 단절점 알고리즘 (0) | 2022.04.05 |
|---|---|
| 힙 정렬 (0) | 2022.03.16 |
| Kruskal Algorithm (0) | 2022.03.02 |
| 플루이드 와샬 (0) | 2022.03.02 |
| Union find (0) | 2022.02.28 |
