특정 정점을 제거했을 때 트리의 수가 증가한다면, 해당 정점을 단절점이라고 표현한다.
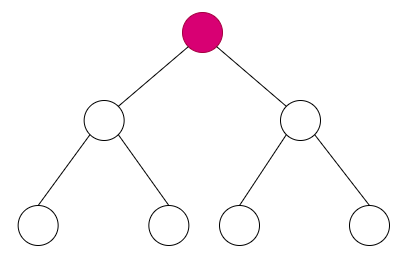
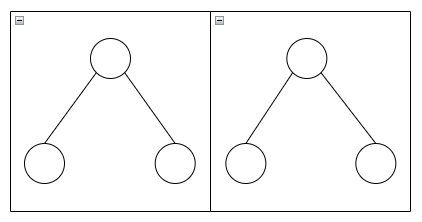
단절점을 구하기 전에 먼저 해야 할 일이 있다. 위와 같은 트리가 주어졌다고 했을 때 우리는 DFS를 수행하면서 방문 순서를 기록해야 한다.
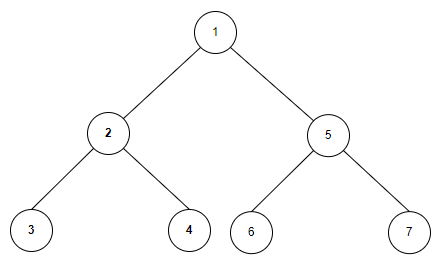
방문 순서를 확인하면 단절점의 특징을 찾을 수 있다.
- 1번 노드는 루트 노드이고 자식 노드가 두 개 이상이다.
- 또한 1번 노드는 단절점이다.
- 2번 노드의 자식 노드들(3, 4)은 2번 노드를 거치지 않고 1번 노드로 갈 수 없다.
- 또한 2번 노드는 단절점이다.
- 5번 노드의 자식 노드들(6, 7)은 5번 노드를 거치지 않고 1번 노드로 갈 수 없다.
- 또한 5번 노드는 단절점이다.
정리해보면
- 루트 노드는 자식 노드가 둘 이상이면 무조건 단절점이다.
- 특정 노드의 자식 노드들이 해당 노드를 거치지 않고 더 빠른 방문순서의 노드로 갈 수 없다면 해당 노드는 단절점이다.
- 즉, 다음과 같은 경우 2번 노드는 단절점이 아니다.
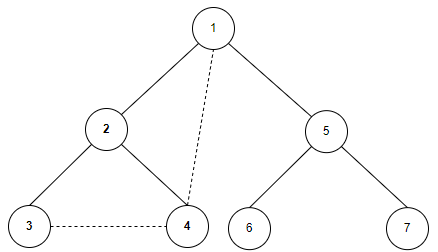
이제 코드로 구현해보자. 코드의 흐름은 간단하다.
루트 노드를 설정하고 주어진 Edge들로 DFS를 수행하며, 자식 노드들로부터 return 되는 방문 값들을 통해서 해당 노드가 단절점인지 아닌지 확인해주면 된다. 루트 노드의 경우 자식 노드가 두 개 이상인지만 확인해주면 된다.
#include <iostream>
#include <vector>
using namespace std;
int root = 1;
int sequence = 1;
int visitSeq[8] = {0};
bool breakPoint[8] = {0};
vector<int> edges[8];
int findBreakPoint(int now) {
// 방문 순서를 기록하고 sequence를 증가시킨다.
int fastestOne = sequence;
visitSeq[now] = sequence++;
// 루트 노드를 위한 childCount
int childCount = 0;
// now 노드와 연결된 간선을 모두 탐색
for(int next : edges[now]) {
// 방문했던 노드라면 방문 순서를 비교해서 더 작은 순서로 갱신
if(visitSeq[next]) {
fastestOne = min(fastestOne, visitSeq[next]);
continue;
}
// 자식(트리) 수 증가
childCount++;
// 방문한 적 없으니 함수 호출(탐색)
int minSeq = findBreakPoint(next);
// 자식 노드들이 방문할 수 있는 노드 중 가장 빠른 순서가 현재 노드 방문 순서보다 낮다면 단절점이므로
if(now != root && visitSeq[now] <= minSeq) {
breakPoint[now] = true;
}
// 더 작은 방문 순서로 갱신
fastestOne = min(fastestOne, minSeq);
}
// 루트 노드인데 자식(트리)가 두개 이상이라면
if(now == root && childCount >= 2) {
breakPoint[now] = true;
}
return fastestOne;
}
int main() {
// 간선 설정
edges[1].emplace_back(2);
edges[1].emplace_back(5);
edges[2].emplace_back(3);
edges[2].emplace_back(4);
edges[5].emplace_back(6);
edges[5].emplace_back(7);
findBreakPoint(1);
for(int i = 1; i < 8; i++) {
if(breakPoint[i])
cout << i << " is breakPoint\n";
else
cout << i << " is not breakPoint\n";
}
}[출력 결과]
___________________
1 is breakPoint
2 is breakPoint
3 is not breakPoint
4 is not breakPoint
5 is breakPoint
6 is not breakPoint
7 is not breakPoint'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 1일 1백준 후기 (2) | 2022.05.14 |
|---|---|
| Binary Indexed Tree (Fenwick Tree) (0) | 2022.04.09 |
| 힙 정렬 (0) | 2022.03.16 |
| 위상 정렬 (0) | 2022.03.11 |
| Kruskal Algorithm (0) | 2022.03.02 |
