Trie 자료구조는 문자열을 저장하고 주어진 문자열에 겹치는 접두사(문자열)가 있는지 빠르게 검색할 수 있는 트리 자료구조이다.
Trie 자료구조가 문자열을 저장하는 방법을 그림으로 살펴보자.
아래 그림은 Trie 자료구조를 이용해서 문자열 "TREE" 와 "TRIE" 를 저장한 모습이다.
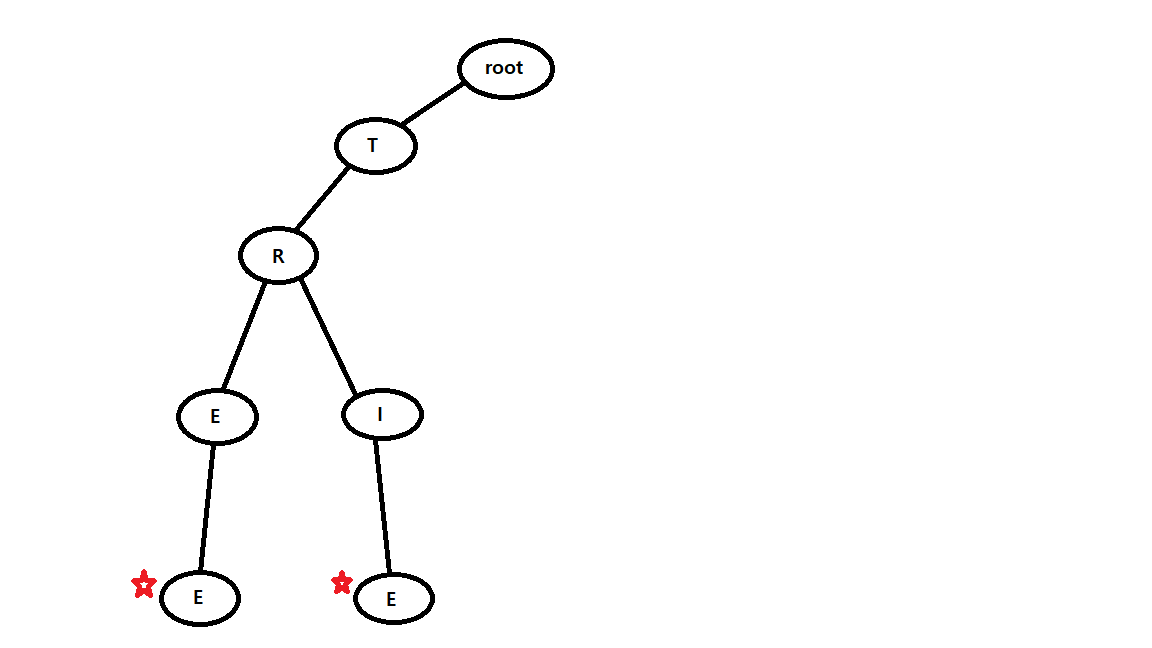
Trie의 특징은 사용하는 문자열 셋(a~f, A~F, '0'~'9') 을 이용해서 자식 노드를 생성한다는 점과 주어진 문자열을 순회하면서 재귀적으로 자식 노드를 생성한다는 것이다.
위에 그림의 경우 A~F 까지의 문자열 셋을 이용하고 문자 단위로 자식 노드가 생성되는 예시이다.
만약 전화번호를 저장한다면? 0~9 까지의 문자열 셋을 이용하는 것이다.
그럼 Trie 자료구조를 구현해보자.
아래는 영어 소문자로 이루어진 문자열을 저장하는 Trie 자료구조이다.
finish는 문자열 저장이 끝나면 그 다음 노드에서 true로 설정된다.
즉, T-R-E-E-finish 설정 순으로 진행되는 것이다.
해당 동작은 insert 함수에 정의한다.
node[26]은 각각 다음 자식 노드의 주소를 가리키며 자식 노드가 없을 경우 NULL로 표현된다.
생성자는 node[26]을 초기화하고 있고
소멸자는 동적 할당했던 노드들을 삭제하고 있다.
// 영어 문자열을 저장하는 Trie 자료구조 예시
struct Trie {
bool finish;
Trie* node[26]; // 알파벳의 개수 26개
Trie() {
finish = false;
fill_n(node, node + 26, nullptr);
}
~Trie() {
for(int i = 0; i < 26; i++)
if(node[i] != NULL)
delete node[i];
}
void insert(char* cstr);
bool find(char* cstr);
}
그다음 insert를 구현해보자.
우선 insert는 주어진 문자열의 문자를 하나씩 순회하면서 재귀적으로 자식 노드를 생성하면 된다.
만약 문자열을 모두 순회했다면 cstr이 '\0' 을 가리킬 것이고, 그때 재귀를 종료하면 된다.
void Trie::insert(char* cstr) {
if(*cstr == '\0') {
finish = true;
return;
}
int cur = *cstr - 'a';
if(node[cur] == NULL) node[cur] = new Trie();
node[cur]->insert(cstr + 1);
}다음 find를 구현해보자
우선 주어진 문자열의 문자를 하나씩 순회하면서 재귀적으로 탐색한다. insert와 비슷하다.
이때 주어진 문자열과 겹치는 접두사가 발견된다면 재귀 탐색을 종료한다.
주어진 문자열의 탐색이 끝나기도 전에 finish flag를 확인하면, 주어진 문자열에 접두사가 있다는 의미이기 때문에 접두사의 여부를 확인할 수 있다.
예를 들어 christmas가 먼저 저장되어 있다고 하자.
우리는 저장된 문자열 중에 christmas tree 문자열과 겹치는 접두사가 있는지 궁금하다.
그럼 christmas tree 문자열을 insert로 저장하고 find 함수로 탐색하다 보면, christma"s" 를 확인한 뒤에 finish 가 true임을 확인할 수 있을 것이다. 그때 우리는 christmas tree 접두사가 Trie 자료구조에 저장되어 있음을 알 수 있다.
bool Trie::find(char* cstr) {
if(*cstr == '\0') return false; // 겹치는 접두사가 없음
if(finish) return true; // 겹치는 접두사가 있음
int cur = *cstr - 'a';
return node[cur]->find(cstr + 1); // 다음 문자 탐색
굉장히 쉽고 효율적인 자료구조이다. 접두사를 탐색하는 문자열 알고리즘 문제에서 유용하게 쓰일 수 있다.
https://www.acmicpc.net/problem/5052
5052번: 전화번호 목록
첫째 줄에 테스트 케이스의 개수 t가 주어진다. (1 ≤ t ≤ 50) 각 테스트 케이스의 첫째 줄에는 전화번호의 수 n이 주어진다. (1 ≤ n ≤ 10000) 다음 n개의 줄에는 목록에 포함되어 있는 전화번호가
www.acmicpc.net
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 위상 정렬 (0) | 2022.03.11 |
|---|---|
| Kruskal Algorithm (0) | 2022.03.02 |
| 플루이드 와샬 (0) | 2022.03.02 |
| Union find (0) | 2022.02.28 |
| 밸만-포드 알고리즘 (0) | 2022.02.24 |
