밸만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로 그래프에 간선이 가중치를 가질 때 최단 거리를 구하는 알고리즘이다. 만약 그래프가 음수 간선을 가질 때 다익스트라 알고리즘 대신 사용하면 된다.
그럼 당연히 드는 의문이 있을 것이다. 다익스트라는 음수 간선이 있을 때 최단 거리를 구하지 못하는가?
- 아니다. 꼭 그런 것만은 아니다. 음수 간선이 있어도 다익스트라가 최단 거리를 구할 수 있다.
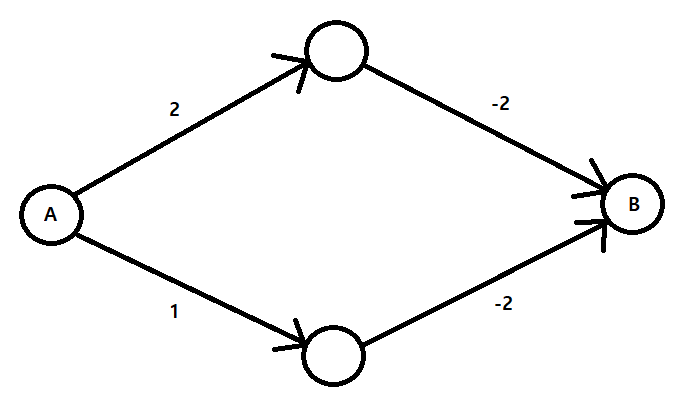
위에 그래프는 단방향의 간선을 가지고 A->B로 가는 경로가 두 가지가 있다. 그래프를 대충 봐도 우리는 당연하게 A->B로 가는 최단 거리가 -1 임을 알 수 있다. 다익스트라도 이 상황에서는 최단 경로를 구할 수 있고, 결국 그래프에 음수 간선이 있더라도 다익스트라로 무조건 풀 수 없는 건 아니라는 뜻이다.
그럼 언제 밸만-포드를 사용해야 하는가?
- 위에 그래프에서 단방향이 아닌 양방향 간선일 경우를 생각해 보자.

위에 그래프를 살펴보면 양방향 간선이 있기 때문에 빨간색 화살표 방향으로 계속 순환할 수 있다. 빨간색 화살표 방향으로 계속 순환하다 보면 우리는 최단 거리가 무한대로 줄어들 수 있음을 알 수 있다. (-1 -> -2 -> -3 -> -4.....) 순환하면 할수록 최단 거리가 줄어든다. 바로 이것을 음수 간선 순환이라고 한다. (음수 사이클이라고도 하는 것 같다)
그래프에 음수 사이클이 존재하는 경우 다익스트라는 절대 최단 거리를 구할 수 없다. 다익스트라 알고리즘을 사용하면 음수 사이클로 인해 거리 배열이 계속 갱신될 수 있기 때문에 무한 루프에 빠지게 된다.
그럼 밸만-포드 알고리즘은 이를 어떻게 극복하는가?
- 밸만-포드 알고리즘은 우선 정점의 개수만큼 반복하고 매 반복에서 모든 간선에 대해 거리를 갱신한다. 그리고 N 번째 시도에서 거리가 갱신된다면 음수 사이클이 있다고 판단한다. 우리는 이를 통해 그래프에 음수 사이클이 있는지 확인할 수 있고 문제 해결에 이용할 수 있다.
( 또는 전체 간선 개수만큼 한 번 더 거리를 갱신해서 확인해 볼 수도 있다 )
나름 직접 짜 본 밸만-포드 알고리즘의 의사 코드 (ㅋㅋ)
edge {
start
end
cost
}
dist[N] = {INF} // 거리 배열 N 개
edge[M] = {...} // 간선 정보 M 개
negativeCirculation = false // 음수 사이클 여부
while ( i < N ) : // N 번 만큼 반복한다
while ( j < M ) : // M 번 만큼 반복한다
if ( dist[edge[j].start] != INF ) : // 아직 갱신되지 않은 정점은 건너뛴다
if ( dist[edge[j].end] > dist[edge[j].start] + edge[j].cost ) : // 최단 거리로 갱신이 가능한지
dist[edge[j].end] = dist[edge[j].start] + edge[j].cost // 갱신
if ( i == N - 1 ) : // N 번째에 갱신된다면
negativeCirculation = true
return나만 알아볼 수 있을 듯..
그래도 난이도가 높지 않은 알고리즘 같다. 다익스트라를 처음 접했을 때보다는 훨씬 쉽다는 느낌이 드는 알고리즘이다.
관련 백준 문제
https://www.acmicpc.net/problem/1865
1865번: 웜홀
첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500),
www.acmicpc.net
내 풀이
https://github.com/seaworld0125/boj-hard-training/blob/main/1865/1865.md
GitHub - seaworld0125/boj-hard-training: 매일 1문제 + 해설
매일 1문제 + 해설. Contribute to seaworld0125/boj-hard-training development by creating an account on GitHub.
github.com
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| 위상 정렬 (0) | 2022.03.11 |
|---|---|
| Kruskal Algorithm (0) | 2022.03.02 |
| 플루이드 와샬 (0) | 2022.03.02 |
| Union find (0) | 2022.02.28 |
| Trie 자료구조 (0) | 2022.02.28 |
