펜윅 트리는 값이 변경되어도 구간의 합을 빠르게 구할 수 있는 자료구조이다. 기존의 구간 합을 구하는 방법은 값의 변경이 있을 때 매번 O(n)의 시간이 걸리지만 펜윅 트리는 O(logn)의 시간이 걸린다. 어떻게 가능한 걸까?
우선 펜윅 트리의 구조를 먼저 그려보고 살펴보자. 펜윅 트리의 특징은 다음과 같다.
- 펜윅 트리는 화살표가 가리키는 곳에 각 구간의 합이 저장된다.
- 조금 헷갈릴 수 있는 부분이 BIT 배열의 인덱스는 0이 아닌 1부터 시작한다. 즉 BIT[1] 에는 원래 배열 arr[0]이 저장된다. BIT[4] 에는 원래 배열 arr[0]~arr[3]의 구간 합이 저장된다.
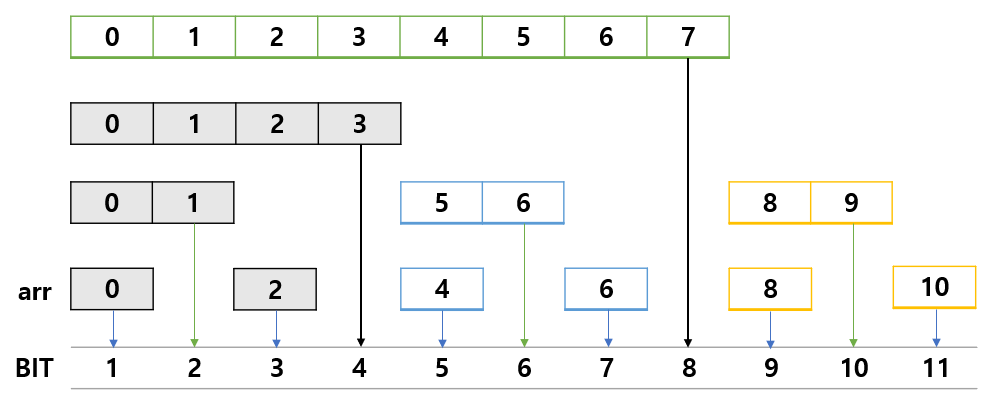
BIT 자료구조를 사용하는 가장 큰 이유는 값의 업데이트와 구간 합을 구하기 위함일 것이다. 값을 어떻게 업데이트하고 합을 구하길래 O(logn)의 시간만 걸리는 걸까...
위 그림에서 arr[3]의 값이 변경되었다고 가정해보자. 그럼 우리가 업데이트해야 하는 값은 BIT[4]와 BIT[8]일 것이다. 즉 두 가지 값만 업데이트하면 구간합을 구할 수 있다(매우 효율적임). 그런데 업데이트해야 하는 Index를 어떻게 구할 수 있을까?
우선 BIT에 맞는 index로 변환해줘야 하기 때문에 원래 배열 인덱스 3에 +1을 해서 4를 구한다. 즉 업데이트되는 인덱스는 4부터 시작되는 것이다. 그다음 8은??
이때 비트 연산이 이용된다. 무슨 소린인가 싶겠지만 일단 4와 8을 이진수로 나타내 보자. 이진수로 나타냈을 때 4의 마지막 비트에 1(의미상 1이다)을 더해주면 8이 된다. 그럼 마지막 비트 값은 어떻게 구할까? 이때 2의 보수를 구해서 & 연산을 해주면 마지막 비트 값이 나온다. (잘 모르겠으면 직접 손으로 계산해보자) 그리고 이 규칙은 BIT에서 값을 업데이트할 때 계속 쓰이는 방법이다.
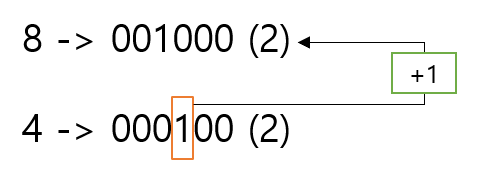
그럼 위에 규칙을 이용하는 업데이트 함수를 작성해보자.
void updateBIT(int originalIdx, int updateNum) {
int idx = originalIdx + 1; // BIT에 인덱스에 맞게 +1
int size = bit.size(); // 인덱스 범위 설정
while(idx <= size) { // 구간합 업데이트
bit[idx] += updateNum;
idx += (idx & -idx);
}
}
그럼 업데이트가 아닌 구간합을 구하는 방법은 어떻게 될까? 원래 배열 0부터 6까지의 구간합을 구한다고 가정해보자. BIT를 이용하면 BIT[7] + BIT[6] + BIT[4]를 구하기만 하면 되는 것이다. 이 또한 이진수로 나타내면 규칙이 나타난다.
7 -> 6 -> 4 -> 0 간의 규칙은 마지막 비트를 제거하면 그다음 숫자가 나온다는 규칙이 있다. 즉 자기 자신의 마지막 비트 값을 빼주면 다음 인덱스를 구할 수 있다. ( 7 - 1 = 6 ) ( 6 - 2 = 4 ) ( 4 - 4 = 0 )

그럼 위에 규칙을 이용하는 구간합 구하기 함수를 작성해보자.
int getSum(int idx) {
idx++; // BIT index에 맞게 변환
int sum = 0; // 구간합
while(idx > 0) {
sum += bit[idx]; // 구간합 누적
idx -= (idx & -idx); // idx 연산
}
return sum;
}
이제 위 함수들을 이용한 BIT 자료구조의 전체 코드를 작성해보자.
#include <iostream>
#include <vector>
using namespace std;
#define MAX 1000001
int arr[MAX]; // original arr
struct BinaryIndexedTree {
vector<int> bit;
BinaryIndexedTree(int size) {
bit.resize(size + 1, 0);
for(int i = 0; i < size; i++) {
this->updateBIT(i, arr[i]);
}
}
void updateBIT(int originalIdx, int updateNum) {
int idx = originalIdx + 1;
int size = bit.size();
while(idx <= size) {
bit[idx] += updateNum;
idx += (idx & -idx);
}
}
int getSum(int idx) {
idx++;
int sum = 0;
while(idx > 0) {
sum += bit[idx];
idx -= (idx & -idx);
}
return sum;
}
};
int main() {
for(int i = 0; i < 12; i++) {
arr[i] = i + 1; // 1부터 11까지 저장
}
BinaryIndexedTree BIT(12);
cout << BIT.getSum(3) << endl; // 3번 인덱스까지의 합 = 1,2,3,4 의 합
BIT.updateBIT(2, 10 - arr[2]); // 2번 인덱스를 10으로 업데이트...
arr[2] = 10;
cout << BIT.getSum(3) << endl; // 3번 인덱스까지의 합 = 1,2,10,4 의 합
BIT.updateBIT(3, -10 - arr[3]); // 3번 인덱스를 -10으로 업데이트...
arr[3] = -10;
cout << BIT.getSum(3) << endl; // 3번 인덱스까지의 합 = 1,2,10,-10 의 합
}// cout...
// arr = {1,2,3,4,5}
10
// arr = {1,2,10,4,5}
17
// arr = {1,2,10,-10,5}
3
위에서 연산 과정을 살펴봤지만 업데이트와 구간합을 구하는데 최대 연산의 횟수가 logn 이하임을 확인할 수 있다. 즉 BIT의 시간 복잡도는 O(logn)이다.
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| Segment Tree (Range Query) (0) | 2022.05.24 |
|---|---|
| 1일 1백준 후기 (2) | 2022.05.14 |
| 단절점 알고리즘 (0) | 2022.04.05 |
| 힙 정렬 (0) | 2022.03.16 |
| 위상 정렬 (0) | 2022.03.11 |
