세그먼트 트리는 sum, sub 연산 말고도
min, max, gcd, lcm과 같은 다양한 연산이 가능한 자료구조이다.
Segment Tree
주어지는 연속된 데이터에 대한 구간 연산(Update, query)을 O(logn) 시간에 할 수 있는 자료구조이다.
다음과 같은 배열이 있다고 하자. (index는 왼쪽부터 0이다)

SUM 연산을 위한 세그먼트 트리는 위 배열을 다음과 같이 표현한다. 표현 방식은 굉장히 간단한데, 각 노드의 자식 노드를 더해서 해당 노드의 값으로 표현한다. 즉 루트 노드는 전체 원소의 합이라고 볼 수 있다. 전체 원소의 합이라는 것은 전체 원소를 cover 한다는 뜻으로 생각하면 된다. 즉, root에서 leaf로 내려갈수록 cover 범위가 줄어든다고 보면 된다.
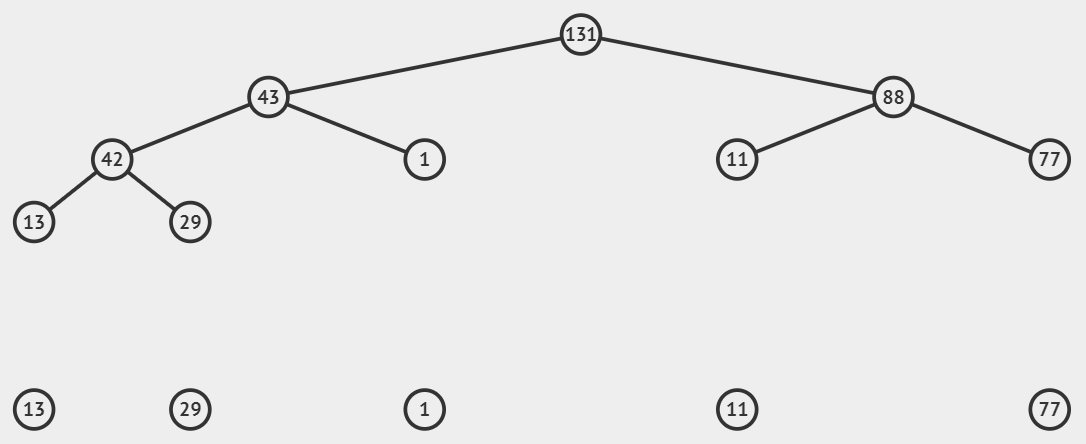
그리고 루트 노드부터 인덱스를 1로 설정하여 노드의 인덱스를 표현한다. 세그먼트 트리는 완전 이진트리의 특성을 가지고 있어서 루트 노드를 1로 설정하면 왼쪽 자식 노드는 * 2를 한 인덱스이고 오른쪽 자식 노드는 * 2 + 1을 한 인덱스여서 쉽게 인덱스를 참조할 수 있다. (그래프를 살펴보면 여러 가지 완전 이진트리의 특성이 나타난다)
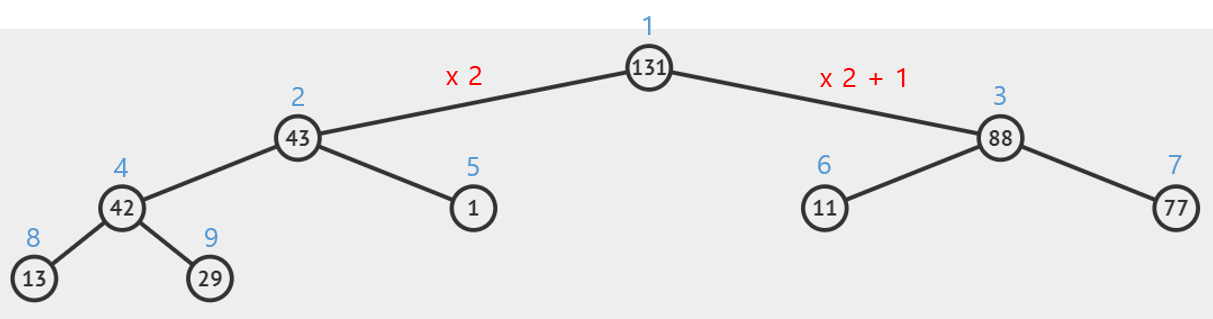
인덱스를 매겼으니 배열로도 표현이 가능하다.
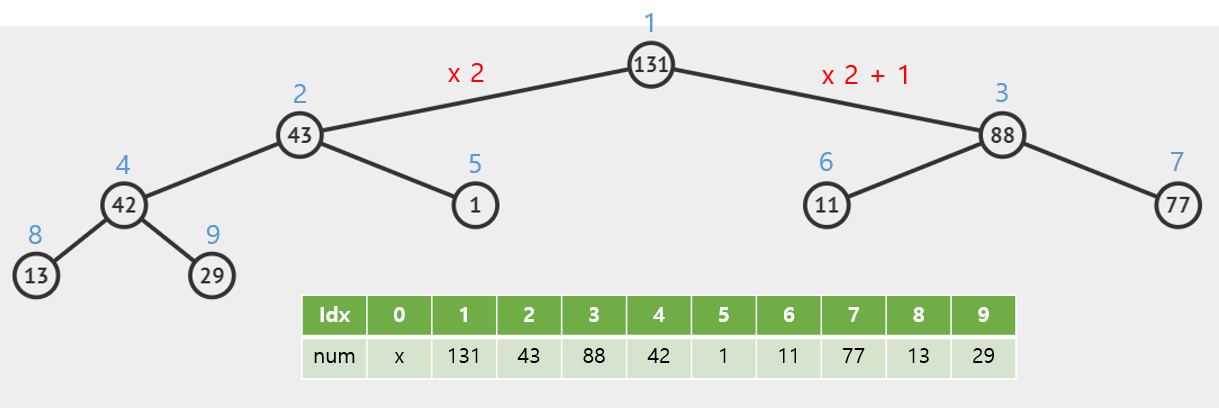
Build
세그먼트 트리를 어떻게 구성하는지 살펴보자. 세그먼트 트리는 분할 정복 기법(재귀)을 활용해서 Build, Query, Update를 수행한다.
struct SegmentTree {
/*
size = 원래 배열의 size
tree = 세그먼트 트리
*/
int size;
vector<int> tree;
// 세그먼트 트리를 구성할 때 사용할 연산
int opt(int left, int right) {
// sum
return left + right;
}
/*
arr = 원래 배열
node = segmentTree 인덱스
left = 현재 segmentTree 노드가 cover하는 원래 배열의 left index
right = 현재 segmentTree 노드가 cover하는 원래 배열의 right index
*/
int buildRecursive(const int arr[], int node, int left, int right) {
// 트리가 더 이상 깊어질 수 없음. 즉 leaf 노드임. leaf 노드는 자신만 cover한다.
if(left == right) {
return tree[node] = arr[left];
}
int mid = (left + right) / 2;
// 왼쪽 자식 노드로 이동
int lVal = buildRecursive(arr, node * 2, left, mid);
// 오른쪽 자식 노드로 이동
int rVal = buildRecursive(arr, node * 2 + 1, mid + 1, right);
return tree[node] = opt(lVal, rVal);
}
/*
세그먼트 트리의 생성자
arr = 원래 배열
size = 원래 배열의 size
*/
SegmentTree(const int arr[], int size) {
this->size = size;
// 세그먼트 트리의 size는 원래 배열 size의 4배를 넘기지 않는다.
this->tree.resize(size * 4);
buildRecursive(arr, 1, 0, size - 1);
}
};
Range Query
range qeury를 처리하는 것도 어렵지 않다. qeury 범위를 벗어난 경우를 recursive의 종료 조건으로 설정하고 범위에 들어온 경우에는 segmentTree에 저장된 값을 그대로 return 하는 식으로 진행하면 된다.
/*
qLeft = query left index
qRight = query Right index
node = 현재 segmentTree node
left = 현재 segmentTree node의 cover left index
right = 현재 segmentTree node의 cover right index
*/
int rangeQuery(int qLeft, int qRight, int node, int left, int right) {
// 범위를 벗어난다면 Query 연산에 영향이 없는 값(0)을 return한다.
if(right < qLeft || qRight < left) {
return 0;
}
// 범위에 들어온다면 segmentTree에 저장되어 있는 값을 return
if(qLeft <= left && right <= qRight) {
return this->tree[node];
}
int mid = (left + right) / 2;
int lVal = rangeQuery(qLeft, qRight, node * 2, left, mid);
int rVal = rangeQuery(qLeft, qRight, node * 2 + 1, mid + 1, right);
return opt(lVal, rVal);
}
Update
update를 처리하는 것도 어렵지 않다. range query와 조금 다를 뿐인데, 범위를 벗어난 경우에 segmentTree의 값을 그대로 return 해줘야 한다. segmentTree에서 수행하는 연산이 sum이라면 0을 리턴해줘도 된다(단순히 더하기만 하면 되기 때문). 하지만 min, max와 같은 연산이라면 왼쪽과 오른쪽 자식 트리로부터 반환되는 값들에 min, max를 수행해주어야 위로 update 되는 값들도 정상적으로 업데이트될 것이다.
/*
updateVal = update value
index = update index
node = 현재 segmentTree node
left = 현재 segmentTree node의 cover left index
right = 현재 segmentTree node의 cover right index
*/
int updateQeury(int updateVal, int index, int node, int left, int right) {
// update index가 현재 범위 밖이라면
if(index < left || right < index) {
return this->tree[node];
}
// update index에 도달했다면
if(left == right) {
return this->tree[node] = updateVal;
}
int mid = (left + right) / 2;
int lVal = updateQeury(updateVal, index, node * 2, left, mid);
int rVal = updateQeury(updateVal, index, node * 2 + 1, mid + 1, right);
return tree[node] = opt(lVal, rVal);
}
전체 코드를 한 번 살펴보자.
#include <iostream>
#include <vector>
using namespace std;
struct SegmentTree {
int size;
vector<int> tree;
int opt(int left, int right) {
// sum
return left + right;
}
int buildRecursive(const int arr[], int node, int left, int right) {
if(left == right) {
return tree[node] = arr[left];
}
int mid = (left + right) / 2;
int lVal = buildRecursive(arr, node * 2, left, mid);
int rVal = buildRecursive(arr, node * 2 + 1, mid + 1, right);
return tree[node] = opt(lVal, rVal);
}
SegmentTree(const int arr[], int size) {
this->size = size;
this->tree.resize(size * 4);
buildRecursive(arr, 1, 0, size - 1);
}
/*
qLeft = query left index
qRight = query Right index
node = 현재 segmentTree node
left = 현재 segmentTree node의 cover left index
right = 현재 segmentTree node의 cover right index
*/
int rangeQuery(int qLeft, int qRight, int node, int left, int right) {
// 범위를 벗어난다면 Query 연산에 영향이 없는 값(0)을 return한다.
if(right < qLeft || qRight < left) {
return 0;
}
// 범위에 들어온다면 segmentTree에 저장되어 있는 값을 return
if(qLeft <= left && right <= qRight) {
return this->tree[node];
}
int mid = (left + right) / 2;
int lVal = rangeQuery(qLeft, qRight, node * 2, left, mid);
int rVal = rangeQuery(qLeft, qRight, node * 2 + 1, mid + 1, right);
return opt(lVal, rVal);
}
/*
updateVal = update value
index = update index
node = 현재 segmentTree node
left = 현재 segmentTree node의 cover left index
right = 현재 segmentTree node의 cover right index
*/
int updateQeury(int updateVal, int index, int node, int left, int right) {
// update index가 현재 범위 밖이라면
if(index < left || right < index) {
return this->tree[node];
}
// update index에 도달했다면
if(left == right) {
return this->tree[node] = updateVal;
}
int mid = (left + right) / 2;
int lVal = updateQeury(updateVal, index, node * 2, left, mid);
int rVal = updateQeury(updateVal, index, node * 2 + 1, mid + 1, right);
return tree[node] = opt(lVal, rVal);
}
};
int main() {
int arr[] = {13, 29, 1, 11, 77};
int size = 5;
SegmentTree segTree(arr, size);
cout << "(2 ~ 3) range sum = " << segTree.rangeQuery(2, 3, 1, 0, size - 1) << endl;
cout << "update arr[3] => 22\n"; segTree.updateQeury(22, 3, 1, 0, size - 1);
cout << "(2 ~ 3) range sum = " << segTree.rangeQuery(2, 3, 1, 0, size - 1) << endl;
}
/*
output
>> (2 ~ 3) range sum = 12
>> update arr[3] => 22
>> (2 ~ 3) range sum = 23
*/
후기
펜윅 트리의 기능을 세그먼트 트리로 대체할 수 있겠지만, 만약에 단순 구간합을 저장하고 더 적은 메모리를 사용하길 원한다면 펜윅 트리를 사용하는 것도 나쁘지 않은 선택인 것 같다.
'알고리즘 & 자료구조 > 개념' 카테고리의 다른 글
| TRIE 자료구조 (0) | 2022.08.04 |
|---|---|
| 1일 1백준 후기 (2) | 2022.05.14 |
| Binary Indexed Tree (Fenwick Tree) (0) | 2022.04.09 |
| 단절점 알고리즘 (0) | 2022.04.05 |
| 힙 정렬 (0) | 2022.03.16 |
